
Vertex Separators
Why
We characterize chordal graphs.1
Definition
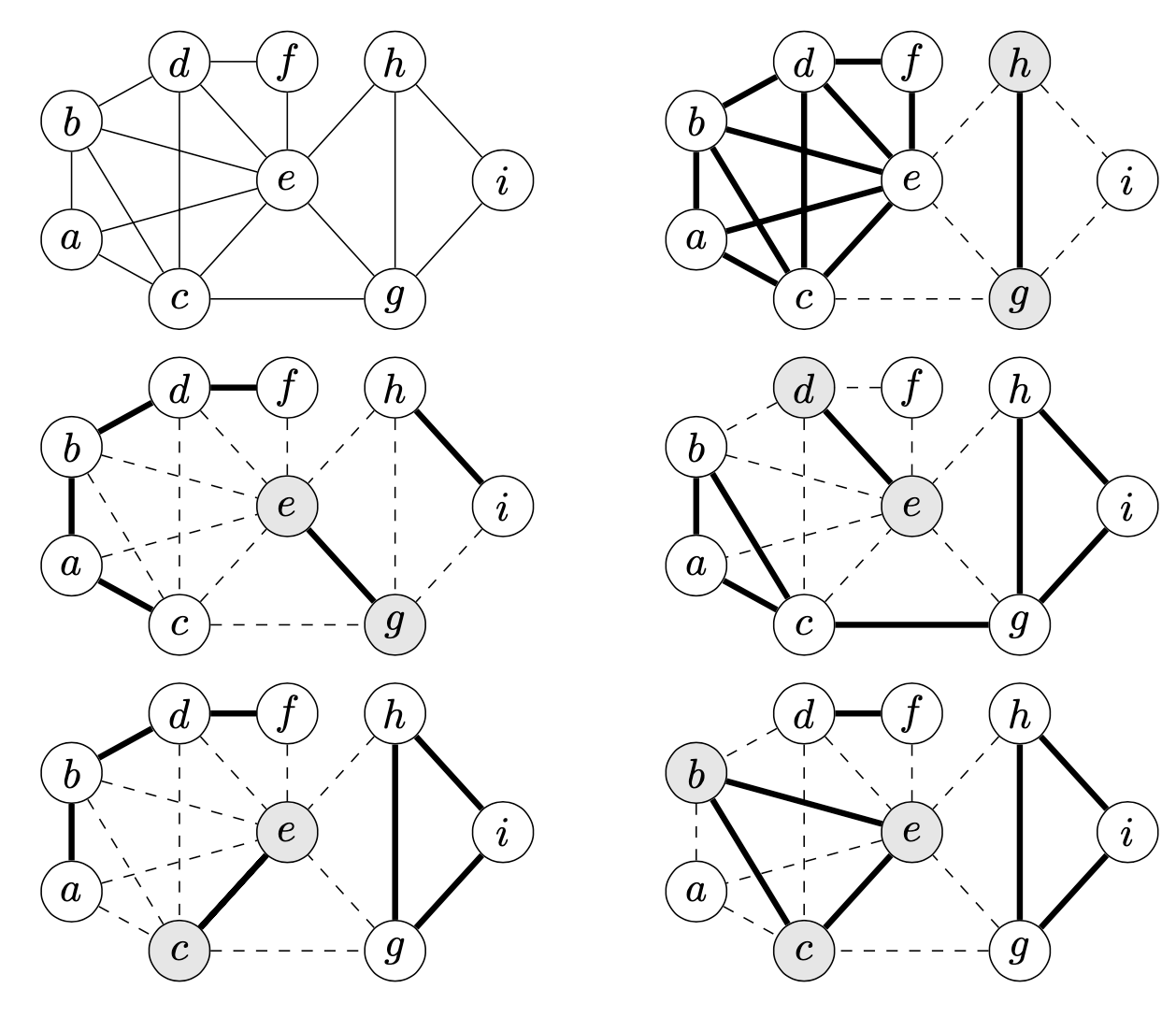
Let $(V, E)$ be an undirected graph. A set $S \subset V$ is a vertex separator for two vertices $v, w$ (or a $vw$-separator) if $v$ and $w$ are disconnected in the subgraph induced by $V \setminus S$. There always exists a vertex separator for two nonadjacent vertices.
A vertex separator is a minimal vertex separator for two vertices if no proper subset of it is a vertex separator for those vertices. Another term for vertex separator is cutset. Similarly, one for minimal vertex separator is relatively minimal cutset.
Example
For example, for the graph in Figure below , $\set{c,e}$ is a minimal $ag$-separator and $\set{b,c,e}$ is a minimal $ad$-separator. A minimal vertex separator may contain another minimal vertex separator if they are minimal for different pairs of vertices.
- Future editions will expand. ↩︎