
Rooted Trees
Why
We want to talk rooting a tree at a given vertex.1
Definition
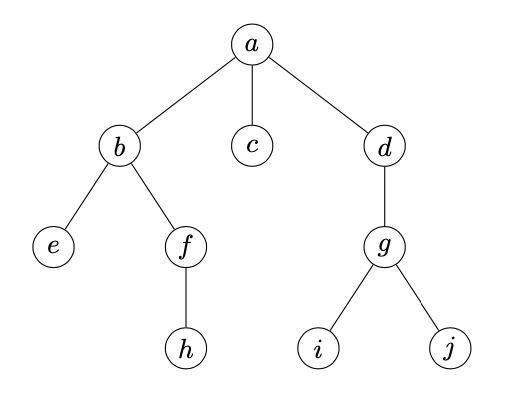
A rooted tree is an ordered pair $((V, T), r)$ where $(V, T)$ is a tree and $r \in V$ is a distinguished vertex which we call the root. We visualize rooted trees with the root at the top (see the figure below).
Parents and children
Suppose $w$ is the first vertex on the path from the root to a non-root vertex $v$. Since there is only one such path, $w$ is unique and we call it the parent of $v$. Conversely, we call $v$ a child of $w$. We denote the set of children of $v$ by $\ch(v)$. A vertex may have no children or it may have many children. If it has no children we call it a leaf.
We define the parent function $\pa: V \to V$ with the convention that the parent of the root is the root. The parent of degree $k$ where $k > 0$ is $\pa^k(x)$ where $\pa^k$ is the composite of $\pa$ with itself $k$ times. So, in particular, $\pa^{k+1}(v) = \pa(\pa^k(v))$. We define the parent of degree $0$ of $v$ to be $v$, and denote it by $\pa^0(v) = v$. For the tree visualized in the figure below, $\pa(i) = g$, $\pa^2(i) = d$, $\pa^3(i) = a$.
If $w = \pa^k(v)$ for some $k \geq 0$, then $w$ is a ancestor of $v$ and $v$ is a descendent of $w$. We use the term proper ancestor and proper descendent if $k > 0$ (i.e., $w \neq v$).
The depth or level of a vertex $v$ is its distance (seeTrees) to the root. We denote the level of a vertex $v$ by $\lev(v)$. The level of the root is $0$. If $\lev(v) = k > 0$, then $\pa^{k}(v)$ is the root. The level function $\lev$ satisfies $\lev(v) = \lev(\pa(v)) + 1$.
- Future editions will expand this intuition. ↩︎