Rooted Tree Orderings
Why
We want to simplify common questions using orderings of a rooted tree.1
Definition
A topological ordering of a rooted tree is an ordering $\sigma $ for which $v \prec_{\sigma } \pa(v)$. If there are $n$ vertices, the root has index $n$ and every other vertex has an index less than its parent.
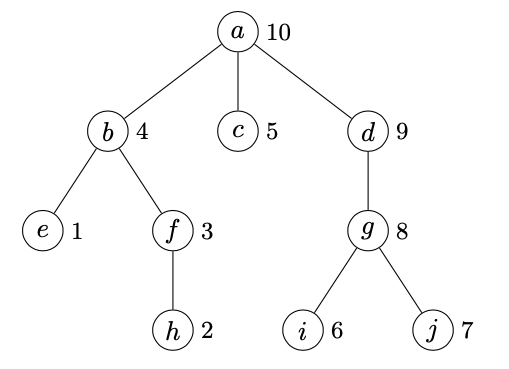
A postordering is a topological ordering in which descendents of a vertex are given consecutive numbers. For the postordering $\sigma $, if $\inv{\sigma }(v) = j$ and $v$ has $k$ proper descendents then the proper descendents of $v$ have are numbered consecutively from $j - k$ through $j -1$. The figure below shows an example.
One can generate a postordering by numbering vertices in decreasing sequence (starting at $n$) in the order they are visited.2
Given an ordering, the first descendent of $v$ (which we denote $\fdesc(v)$) is the descendent with the lowest index. Given a postordering $\sigma $, one can check whether a vertex $w$ is a proper descendent of $v$, by $\fdesc(v) \preceq_{\sigma } w \prec_{\sigma } v$.