Nonnegative Polynomials

Definition

A polynomial $p: \R \to \R $ is nonnegative (a nonnegative polynomial, nonnegative real polynomial) if

\[ p(x) \geq 0 \quad \text{for all } x \in \R \]

Testing nonnegativity

Given polynomial $p$, how do we know if $p$ is (globally) nonnegative? Consider $p: \R \to \R $ defined by

\[ p(x) = 5x^4 - 4x^3 - x^2 + 2x + 2 \]

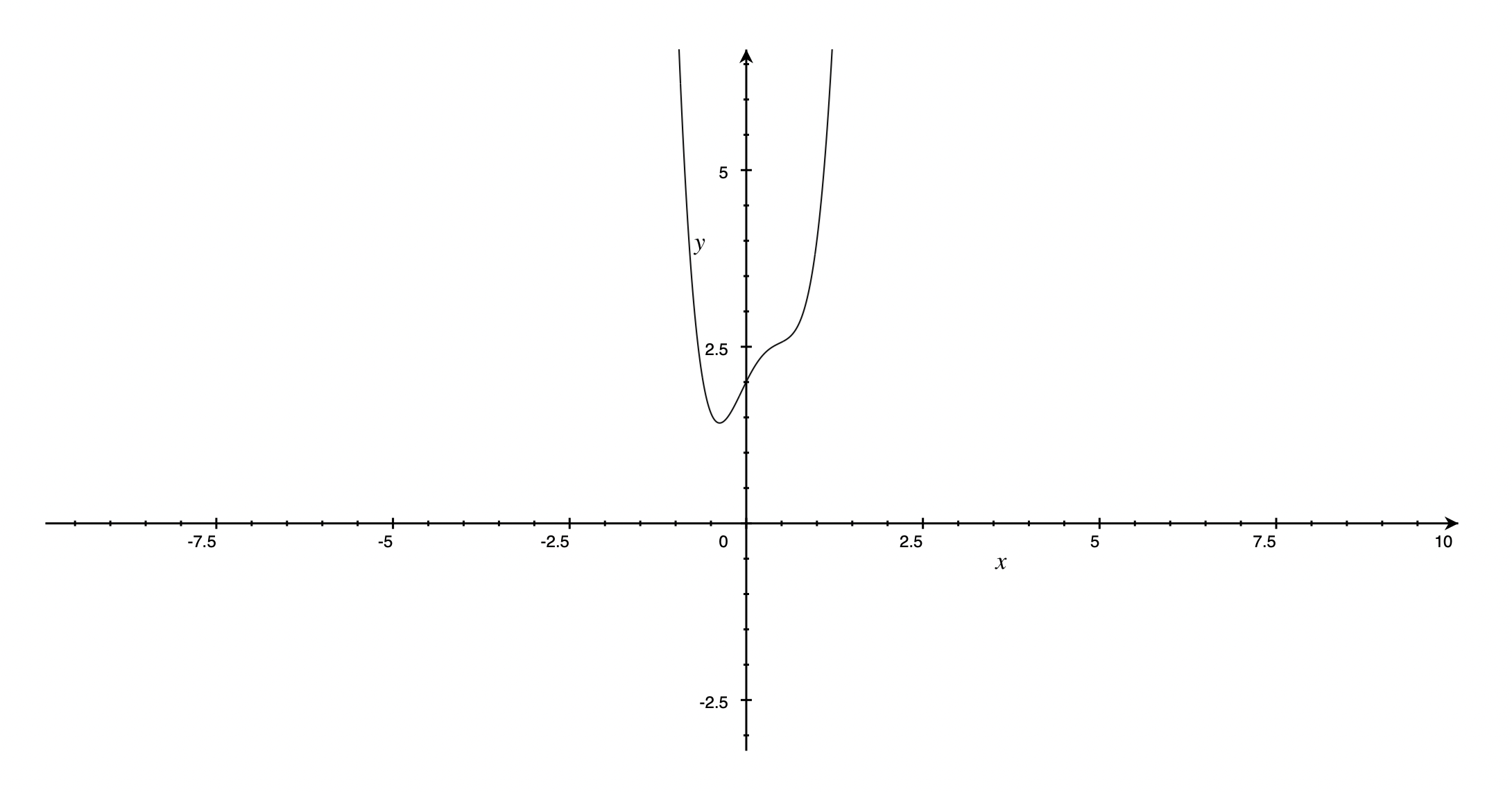
Given the coefficients of $p$, namely the list $(2, 2, -1, -4, 5) \in \R ^5$, how can we tell? It is not so obvious, but if we write

\[ p(x) = (x^2 + 1)^2 + (2x^2 - x - 1)^2, \]

We can ask two questions:

1. If $p$ is a nonnegative polynomial, can it be written as a sum of squares?
2. If $p$ is a sum of squares, how do we find them?