Complex Plane

Why

We regularly visualize $\C $ as a plane.

Definition

Since $\C = \R ^2$, we can identify elements of $\C $ with points in the plane (as we did in Real Plane). In this case, if $z = x + iy \in \C $ (i.e, $z = (x, y) \in \R ^2$), we can visualize this identification in the following figure.

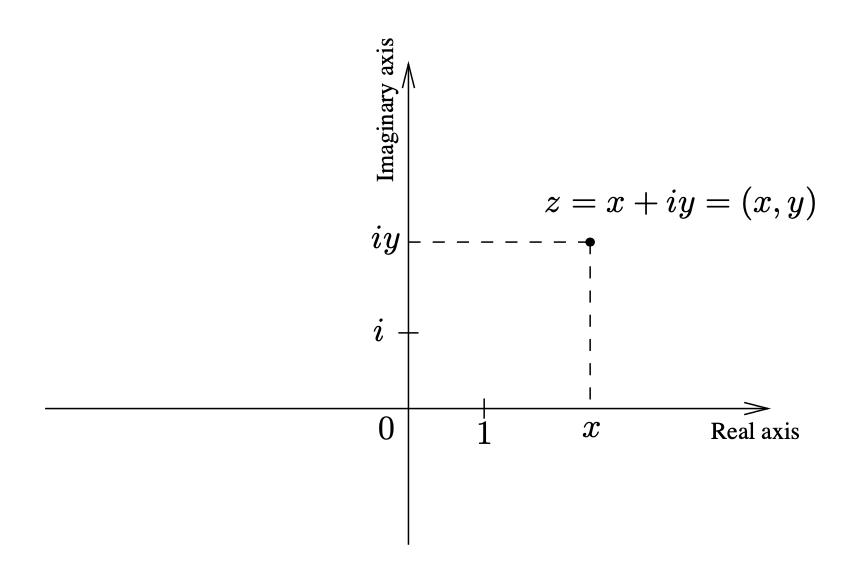
We identify the origin with the complex number $(0, 0) = 0 \in \C $ and for this reason call $0 \in \C $ the complex origin. Likewise, the imaginary number $(0, 1) = i \in \C $ corresponds to $(0,1)$ The horizontal axis corresponds to the purely real numbers and the vertical axis corresponds to the purely imaginary numbers. For these reasons, we refer to these axes as the real axis and imaginary axis, respectively. We refer to the above figure as the complex plane (or Argand diagram).