
Chordal Graphs
Why
Many problems simplify if the graph involved is chordal.1
Paths
Let $G$ be an undirected graph. A chord in a path $p$ of $G$ is an edge between two non-consecutive vertices of $p$. So a chord of the path $(v_1, v_1, \dots , v_{k})$ is an edge $\set{v_i, v_j}$ with $\abs{j - i} > 1$.
We interpret a chord as a “one-edge shortcut” between two vertices of a path. If a path $p$ has a chord, it can be reduced to a shorter path $p'$ by “skipping” vertices. In other words, the shortest path between two vertices is chordless. However, a chordless path need not be a shortest path. See the figure below.
Graphs
A chord of a cycle $(v_1, v_2, \dots , v_{k-1}, v_1)$ is an edge $\set{v_i, v_j}$ with $(j - i) \mod k > 1$. An undirected graph $G$ is chordal if every cycle with more than three edges has a chord.
If $G$ is chordal, every cycle in $G$ can be reduced to a cycle of length three. We sometimes call a cycle of length three a triangle. For this reason, chordal graphs are also sometimes called triangulated graphs. Other terminology includes rigid-circuit graphs, triangulated graphs, perfect elimination graphs, decomposable graphs.2
The last graph in the figure below is not chordal because the cycle $(a, b, d, c, a)$ has length four and no chord. Adding the edge $\set{b, c}$ or $\set{a, d}$ would make the graph chordal An immediate consequence of the definition that $G$ be chordal is that any subgraph of $G$ is chordal.
Simple examples
Since trees and forests have no cycles, they are chordal. Similarly, any graph with no cycles longer than three edges are trivially chordal. Such graphs are sometimes called cactus graphs. The complete graphs are also trivially chordal.
Specific example
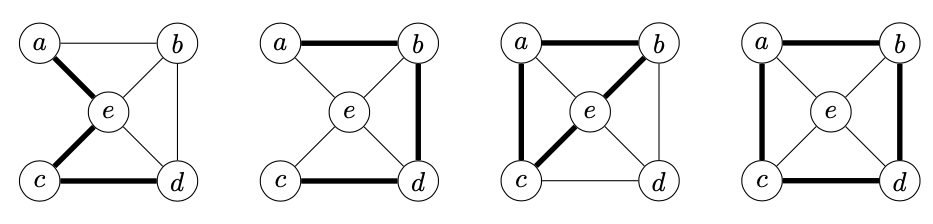
The edge $\set{e, d}$ is a chord in the path $(a, e, c, d)$ of the first graph. The path $(a, v, d, c)$ is chordless. The edge $\set{a, e}$ is a chord in the cycle $(a, v, e, c, a)$ of the second graph. The cycle $(a, b, d, c, a)$ is chordless.